Activation Function: Formulas, Explanation, Usage, Pros and Cons with its Types.

 

Activation functions are an essential component in artificial neural networks, especially in deep learning models. They introduce non-linearity to the network, allowing it to learn complex relationships between input and output. Each neuron in a neural network typically uses an activation function to determine whether and to what extent the information it receives should be passed on to the next layer.

An activation function takes the weighted sum of inputs and the bias term in a neuron and transforms it into the output of the neuron.

It introduces non-linearity to the neural network, enabling it to model and learn complex patterns from the data.

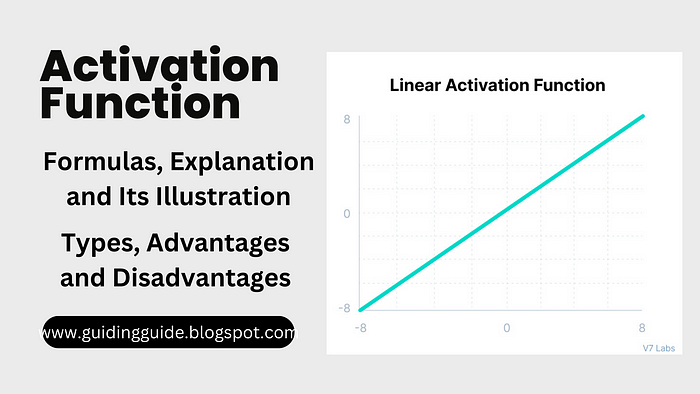
Linear Activation Function

The linear activation function, also known as the identity activation function, is a straightforward and simple activation function used in neural networks. It performs a linear mapping of the input to the output, which means the output is directly proportional to the input. Mathematically, the linear activation function can be defined as:

f(x) = x

Where: f(x) is the output value of the activation function. x is the input value to the activation function.

Advantages of Linear Activation Function:

1. Simplicity: Linear activation functions are straightforward and easy to implement.
2. Preserving Scale: It preserves the scale of the input data, as the output is directly proportional to the input.
3. No Vanishing or Exploding Gradient: The gradient of the linear activation function is constant and does not cause vanishing or exploding gradient issues.

Disadvantages of Linear Activation Function:

1. Lack of Non-linearity: The main drawback of the linear activation function is its lack of non-linearity. Neural networks with only linear activation functions are not able to learn and represent complex relationships in the data.
2. Limited Representation: Due to the absence of non-linearity, a neural network with only linear activation functions is limited in its ability to approximate complex functions.

Where to Use Linear Activation Function: The linear activation function is mainly used in output layers of regression tasks, where the goal is to predict a continuous value. In regression problems, there is no need for non-linearity in the output, as the target variable is continuous, and the model aims to learn a direct mapping from input to output.

For example, in a neural network used for predicting house prices based on features like area, number of rooms, etc., the output layer may use a linear activation function to produce the predicted price directly.

However, in hidden layers, it is generally better to use non-linear activation functions like ReLU, sigmoid, or tanh to introduce non-linearity and enable the neural network to learn complex patterns and relationships in the data. A combination of linear and non-linear activation functions in hidden layers helps in creating powerful and flexible neural network architectures.

Binary Step Activation Function

The step activation function is a simple threshold-based activation function used in neural networks and other machine learning algorithms. It takes an input value and outputs either 0 or 1 based on whether the input is above or below a specified threshold. It is one of the earliest activation functions used in artificial neural networks.

The step activation function can be defined as follows:

f(x) = { 1, if x >= 0 0, if x < 0 }

Where: f(x) is the output value of the activation function. x is the input value to the activation function.

Advantages of Step Activation Function:

1. Simplicity: The step function is straightforward and computationally efficient.
2. Binary Output: It produces a binary output (0 or 1), which can be useful for certain applications that require discrete decisions.

Disadvantages of Step Activation Function:

1. Lack of Continuity: The step function is not continuous, and it has a sharp transition at the threshold. This lack of continuity can cause challenges during gradient-based optimization methods used for training neural networks, leading to instability during training.
2. No Gradient: The step function has no gradient except at the threshold, which makes it unsuitable for backpropagation-based learning algorithms used in most deep learning models.
3. Limited Usefulness: The step activation function is rarely used in modern deep learning architectures due to its limitations, especially in complex tasks where continuous and differentiable activation functions are preferred.

Where to Use Step Activation Function: The step activation function finds limited use in specific scenarios where a binary output is required, such as binary classification problems with simple perceptron models. However, even in such cases, the step function is not commonly used today, as more advanced activation functions, like sigmoid, tanh, or ReLU, are widely available and offer better performance in most cases.

For most deep learning tasks, especially in multi-layered neural networks, it is recommended to use activation functions with continuous and differentiable properties, as they facilitate efficient gradient-based optimization and allow the network to learn complex patterns from data. Non-linear activation functions like ReLU, sigmoid, and tanh are preferred choices in modern neural network architectures.

Sigmoid/ Logistic Activation Function

The sigmoid activation function, also known as the logistic activation function, is a popular non-linear activation function used in artificial neural networks. It maps the input to an output in the range (0, 1), which makes it suitable for binary classification problems and other tasks where probabilistic outputs are desired.

The sigmoid activation function can be defined as follows:

f(x) = 1 / (1 + e^(-x))

Where: f(x) is the output value of the activation function. x is the input value to the activation function. e is Euler’s number (approximately 2.71828).

Advantages of Sigmoid Activation Function:

1. Non-linearity: The sigmoid function introduces non-linearity to the neural network, enabling it to learn and represent complex relationships in the data.
2. Smooth Gradient: The sigmoid function has a smooth, continuous gradient, which makes it suitable for gradient-based optimization algorithms used in training neural networks (e.g., backpropagation).
3. Probability Interpretation: The output of the sigmoid function can be interpreted as a probability, which is useful in binary classification tasks where the network’s output can represent the likelihood of a certain class.

Disadvantages of Sigmoid Activation Function:

1. Vanishing Gradient: The sigmoid function suffers from the vanishing gradient problem, especially for extreme values of input. During backpropagation, gradients can become very small, which hinders learning in deep networks.
2. Output Saturation: The sigmoid function’s output tends to saturate at 0 and 1 for large positive and negative inputs, leading to slower learning and decreased sensitivity to changes in the input.

Where to Use Sigmoid Activation Function: The sigmoid activation function was commonly used in the past for hidden layers in neural networks. However, due to its vanishing gradient issue, it is less favored in deeper architectures. It still finds use in the output layer of binary classification problems, where the goal is to predict the probability of a binary outcome (e.g., predicting whether an email is spam or not). In this case, the sigmoid function ensures that the output is within the range [0, 1], representing the probability of belonging to the positive class.

For hidden layers in modern neural networks, activation functions like ReLU (Rectified Linear Unit) and its variants are more commonly used, as they alleviate the vanishing gradient problem and offer faster convergence during training. ReLU-based activations are known for their ability to efficiently learn complex representations and have become the default choice for many deep learning tasks.

TanH Activation Function (Hyperbolic Tangent)

The hyperbolic tangent activation function, often abbreviated as TanH, is another popular non-linear activation function used in artificial neural networks. Similar to the sigmoid function, it maps the input to an output in the range (-1, 1). It overcomes some of the limitations of the sigmoid function, making it a preferred choice for certain applications.

The hyperbolic tangent activation function can be defined as follows:

f(x) = (2 / (1 + e^(-2x))) — 1

Where: f(x) is the output value of the activation function. x is the input value to the activation function. e is Euler’s number (approximately 2.71828).

Advantages of TanH Activation Function:

1. Non-linearity: Like the sigmoid function, TanH introduces non-linearity to the neural network, allowing it to learn complex patterns and relationships in the data.
2. Zero-Centered Output: The output of the TanH function is centered around zero, which can help with faster convergence during the learning process.
3. Smooth Gradient: The TanH function has a smooth, continuous gradient, making it suitable for gradient-based optimization algorithms used in training neural networks (e.g., backpropagation).

Disadvantages of Tanh Activation Function:

1. Vanishing Gradient: Although the TanH function mitigates the vanishing gradient problem better than the sigmoid function, it can still suffer from this issue for very large or very small input values.
2. Output Saturation: Similar to the sigmoid function, the TanH function’s output can saturate for extreme input values, leading to slower learning and decreased sensitivity to changes in the input.

Where to Use TanH Activation Function: The TanH activation function is widely used in various neural network architectures, especially in recurrent neural networks (RNNs) and Long Short-Term Memory (LSTM) networks. In these cases, the zero-centered output of TanH helps with maintaining the state and reducing the vanishing gradient problem during training.

It can also be used in hidden layers of feedforward neural networks, although some researchers and practitioners prefer the Rectified Linear Unit (ReLU) and its variants due to their ability to address the vanishing gradient problem more effectively and promote faster convergence in deeper architectures.

Overall, TanH is a valuable activation function for certain applications, particularly when zero-centered outputs are desired, and its non-linearity is essential for modeling complex relationships in the data. However, it is essential to consider the specific characteristics of the problem and the architecture of the neural network when selecting the appropriate activation function.

Rectified Linear Unit (ReLU)

The Rectified Linear Unit (ReLU) is a widely used non-linear activation function in deep learning. It introduces simplicity and efficiency to neural networks while addressing some of the limitations of other activation functions like sigmoid and TanH.

The ReLU activation function can be defined as follows:

f(x) = max(0, x)

Where: f(x) is the output value of the activation function. x is the input value to the activation function.

Advantages of ReLU Activation Function:

1. Non-linearity: ReLU introduces non-linearity, enabling neural networks to learn and model complex relationships in the data.
2. Simplicity: ReLU is computationally efficient and easy to implement, making it attractive for large-scale deep learning models.
3. Avoiding Vanishing Gradient: Unlike sigmoid and TanH, ReLU does not suffer from the vanishing gradient problem for positive input values. This accelerates the learning process, especially in deeper networks.
4. Sparse Activation: ReLU activation leads to sparse activation of neurons since any negative input value is mapped to zero. This sparsity can be advantageous in certain cases, making the network more efficient and easier to optimize.

Disadvantages of ReLU Activation Function:

1. Dead Neurons: The main drawback of ReLU is the occurrence of “dead neurons.” When a large negative value is passed through ReLU, the neuron becomes inactive and stops learning (outputting zero) during training. This can result in a dead subnetwork that does not contribute to learning.
2. Exploding Gradient: ReLU can suffer from the exploding gradient problem for very large positive input values.

Where to Use ReLU Activation Function: ReLU is commonly used as the activation function for hidden layers in most deep learning architectures. Its advantages in terms of non-linearity, computational efficiency, and avoiding the vanishing gradient problem have made it the default choice in many neural networks.

However, due to the issue of dead neurons, variations of ReLU have been proposed to address this limitation. Some popular variants include:

1. Leaky ReLU: It allows a small, non-zero gradient for negative inputs to prevent dead neurons. The formula is f(x) = max(ax, x), where a is a small positive constant (e.g., 0.01).
2. Parametric ReLU (PReLU): Similar to Leaky ReLU but with the parameter learned during training rather than fixed.
3. Exponential Linear Unit (ELU): It has a smooth curve for both positive and negative inputs, which helps alleviate the dead neuron problem and can reduce the likelihood of the exploding gradient issue.

ReLU and its variants have proven to be effective choices for most deep-learning tasks, and selecting the appropriate activation function often depends on the specific problem, architecture, and performance requirements.

Softmax Activation Function

The softmax activation function is a widely used activation function, especially in multi-class classification problems. It takes a vector of real numbers as input and transforms them into a probability distribution, where the output values represent the likelihood of each class being the correct class. It is commonly used in the final layer of a neural network for multi-class classification tasks.

The softmax activation function can be defined as follows:

Given an input vector z = [z1, z2, …, zn], the softmax function calculates the probability (p_i) of each element (z_i) as:

p_i = e^(z_i) / sum(e^(z_j)) for j = 1 to n

Where: p_i is the output probability for class i. z_i is the input value for class i. e is Euler’s number (approximately 2.71828).

Advantages of Softmax Activation Function:

1. Probability Interpretation: Softmax converts the input values into probabilities, making it suitable for multi-class classification tasks where each class should have a probability score indicating its likelihood of being the correct class.
2. Normalization: The softmax function normalizes the output probabilities, ensuring that they sum to 1, which represents a valid probability distribution.

Disadvantages of Softmax Activation Function:

1. Sensitivity to Outliers: Softmax is sensitive to outliers in the input vector. Large input values can result in very high probabilities, which might lead to more significant errors during training and inference.
2. Non-Robust to Large Inputs: The exponential operation in the softmax function can cause numerical instability when dealing with large input values.

Where to Use Softmax Activation Function: The softmax activation function is typically used in the final output layer of a neural network for multi-class classification tasks. It is particularly well-suited for problems where an input sample belongs to one and only one class (i.e., exclusive classification).

Applications of the softmax activation function include image classification, natural language processing tasks like sentiment analysis and language translation, and any other tasks that require classifying input data into multiple distinct categories.

It’s important to note that softmax should not be used in hidden layers of a neural network, as it will force the network to make exclusive decisions at each layer, limiting its representational capacity. For hidden layers, non-linear activation functions like ReLU or its variants are commonly used to introduce non-linearity and enable the network to learn more complex patterns in the data.

Conclusion:

In conclusion, activation functions play a crucial role in neural networks by introducing non-linearity and enabling the network to learn complex patterns from the data. Among the commonly used activation functions are:

Sigmoid (Logistic) Activation Function: It maps the input to a range of (0, 1) and was historically popular in the past. However, it has limitations such as vanishing gradient and output saturation, leading to reduced usage in modern architectures.


TanH (Hyperbolic Tangent) Activation Function: Similar to the sigmoid function but with outputs in the range of (-1, 1), TanH addresses some of the issues of sigmoid but still suffers from vanishing gradients.


ReLU (Rectified Linear Unit) Activation Function: ReLU is widely used in hidden layers due to its simplicity, computational efficiency, and avoidance of the vanishing gradient problem for positive input values. However, it may lead to dead neurons and suffer from the exploding gradient issue for large positive inputs.


Softmax Activation Function: Softmax is mainly used in the output layer for multi-class classification tasks, providing a probability distribution over the classes and normalizing the outputs to sum up to 1.

Overall, the choice of activation function depends on the specific problem, network architecture, and performance requirements. Modern architectures often use ReLU or its variants in hidden layers for their effectiveness in training deep networks, while softmax is used in the output layer for multi-class classification tasks. Careful consideration of the activation function is essential to ensure the successful training and performance of neural networks in various applications.